II.1. Grundsätzliches zu Abbildungen

"Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin wird abgebildet?") und der Abbildungs- oder Funktionsvorschrift ("Wie wird abgebildet?").

In unserem Fall besteht sowohl die Definitions- wie die Wertemenge aus den Punkten der Ebene und später aus den Punkten des Raumes. Wir betrachten dabei nur bijektive Abbildungen, d.h. solche, die jeden Punkt einem und nur einem Punkt zuordnen. Man spricht auch von umkehrbar eindeutigen Zuordnungen. Solche Abbildungen besitzen immer eine Umkehr-Abbildung. Die Hintereinanderausführung ("HAF") von Abbildung und Umkehr-Abbildung ergibt die identische Abbildung, bei der jeder Punkt auf sich selbst abgebildet wird.

Wir werden Abbildungen (außer der identischen Abbildung id) mit kleinen griechischen Buchstaben bezeichnen: s (Sigma), t (Tau), d (Delta) und ihre Umkehr-Abbildungen mit s ^-1 etc..

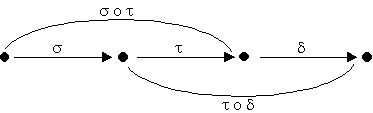
Die HAF von s und t ("erst s, dann t") bezeichnen wir mit s o t.

Demnach gilt: t ist Umkehr-Abbildung von s genau dann, wenn s o t = t o s = id.

Die HAF ist assoziativ, d.h. wenn man drei beliebige Abbildungen s , t , d hintereinander ausführt, dann kann man zum einen s o t als neue Abbildung j auffassen und erst j und dann d ausführen (j o d ), oder man fasst t o d als neue Abbildung y auf und führt sie nach s aus (s o y ): Die resultierende Abbildung ist die selbe. Kurz: Es gilt immer (s o t) o d = s o (t o d).

Bisher ist noch keinerlei geometrische Struktur ins Spiel gekommen. Wir betrachten nur solche Abbildungen, die Geraden in Geraden abbilden ("geradentreue Abbildungen" oder "Kollineationen"). Selbst diese Menge von Abbildungen ist für unsere Zwecke noch zu groß, so dass wir weitere Einschränkungen vornehmen.

Dabei spielen Fixelemente eine besondere Rolle, das sind Punkte, aber auch Linien oder Figuren, die bei der Abbildung unverändert ("invariant") bleiben, d.h. auf sich selbst abgebildet werden.

<<