Winkel am Kreis

Im Kreis sind alle Radien gleich lang. Verbindet man die Kreispunkte, dann bildet die Sehne zusammen mit den beiden Radien ein gleichschenkliges Dreieck. Aus diesem simplen Sachverhalt können wir mit Hilfe der Eselsbrücke eine Reihe von Aussagen über Winkel am Kreis herleiten.

Die Umkehrung lässt sich am besten so einsehen: Zeichnen Sie einen Kreis und einen Durchmesser sowie einen Punkt innerhalb des Kreises (1. Fall) bzw. außerhalb des Kreises (2. Fall). Verbinden Sie diesen Punkt mit den Enden des Durchmessers.
Warum ist der so gebildete Winkel größer bzw. kleiner als ein rechter Winkel?

Verallgemeinerungen des Satzes von Thales und seiner Umkehrung sind:

Umfangswinkelsatz:

• Im Kreis sind die Umfangswinkel über derselben Sehne (über demselben Bogen) gleich.

Umkehrung des Umfangswinkelsatzes:

• Alle Punkte, von denen aus man eine Strecke unter demselben Blickwinkel sieht, liegen auf einem Kreis.

Der Umfangswinkelsatz folgt unmittelbar aus dem

Satz vom Mittelpunktswinkel:

• Im Kreis ist der Mittelpunktswinkel doppelt so groß wie der Umfangswinkel, wenn beide über derselben Sehne (über demselben Bogen) liegen.

Der Beweis dieses Satzes benutzt die Strategie: erst den Spezialfall, dann den allgemeinen Fall durch Rückführung auf den Spezialfall.

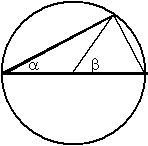
Der Spezialfall	Der allgemeine Fall mit drei Fallunterscheidungen

<<   >>
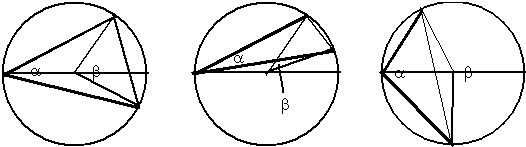