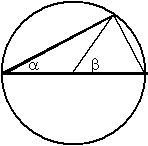
Folgerungen aus dem Umfangswinkelsatz
- Umfangswinkel auf verschiedenen Seiten derselben
Sehne ergänzen sich zu 180°.
- Zu gleich langen Sehnen gehören gleich große
Umfangswinkel und umgekehrt.
Hoppla! Die letzte Aussage ist in dieser Formulierung falsch, obwohl sie einen richtigen
Sachverhalt meint. Finden Sie ein Gegenbeispiel, das die Falschheit der Aussage beleg?
Können Sie die Aussage so korrigieren, dass sie allgemeingültig ist?
Eine Tangente steht senkrecht auf dem Berührradius. Zeichnet man in den beiden Endpunkten einer Sehne die Tangenten, dann gilt der
Satz vom Sehnen-Tangenten-Winkel
- Die beiden Sehnen-Tangenten-Winkel sind gleich
dem Umfangswinkel über der Sehne.
Zeichne einen Kreis mit festem Radius und eine
Sehne AB sowie einen dritten Punkt C auf dem Kreis. Zeichne Winkel ACB und seine Winkelhalbierende.
Die Winkelhalbierende schneidet den Kreis noch in einem zweiten Punkt, nenne ihn D.
Nun bewege C auf dem Kreis. Was passiert mit D? Begründe, was du siehst.
<< >>