
Vierecke mit Umkreis
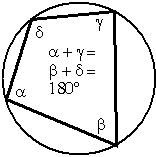
Nicht nur Dreiecke besitzen einen Umkreis. Ein Viereck mit Umkreis heißt auch Sehnen-Viereck. Aus dem Umfangswinkelsatz folgt der
Satz vom Sehnen-Viereck:
Es gilt auch die Umkehrung.
Ein Parallelogramm besitzt nur dann einen Umkreis, wenn es ein
Rechteck ist.
Nicht jedes Trapez, nicht jeder Drachen besitzt einen Umkreis. Unter welchen zusätzlichen Bedingungen doch?
Zeichne einen Kreis mit festem Radius und darin ein Sehnen-Viereck ABCD.
Zeichne die Winkelhalbierenden der Innenwinkel des Sehnen-Vierecks. Die Schnittpunkte der Winkelhalbierenden
benachbarter Winkel bilden ein Viereck EFGH.
Besitzt EFGH einen Umkreis?
Kann EFGH ein Quadrat sein?
Findest du weitere Aussagen über EFGH?
Mit Tricks und Trigonometrie (vgl. H.S.M Coxeter, S.L. Greitzer: Zeitlose Geometrie, Stuttgart 1993) beweist man die
Flächenformel von Brahmagupta für das Sehnenviereck:
Wenn das Sehnen-Viereck zu einem Dreieck entartet, indem z.B. d = 0 wird, ergibt sich die
Flächenformel von Heron für das Dreieck: