
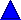

Kosinussatz
Die Verallgemeinerung des Satzes von Pythagoras, die im Falle des spitzwinkligen und des stumpfwinkligen Dreiecks aus der Ungleichung wieder eine Gleichung macht, ist der
Kosinussatz
Im stumpfwinkligen Dreieck ist das Quadrat über der dem stumpfen Winkel gegenüberliegenden
Seite größer als die beiden Quadrate über den anliegenden Seiten zusammen, und
zwar um die doppelte Fläche des Rechtecks, gebildet aus einer anliegenden Seite
und der durch die Höhe auf diese Seite außen abgeschnittenen Strecke an der
stumpfen Ecke.
Im spitzwinkligen Dreieck ist das Quadrat über einer einem spitzen Winkel gegenüberliegenden Seite kleiner als die beiden Quadrate über den anliegenden Seiten zusammen, und zwar um die doppelte Fläche des Rechtecks, gebildet aus einer anliegenden Seite und der durch die Höhe auf diese Seite innen abgeschnittenen Strecke an der spitzen Ecke.
Es gibt etliche Möglichkeiten, den Kosinussatz zu beweisen. Der folgende
Beweis gibt die geometrischen Aussagen besonders gut wieder.
Über den Dreieckseiten werden zunächst die Quadrate ABED,
BCGF und ACHK gezeichnet. Dann werden die Höhen des Dreiecks eingezeichnet
und bis zu den gegenüberliegenden Quadratseiten verlängert. Beim
spitzwinkligen Dreieck teilen die Höhen die Quadrate so in zwei Rechtecke.
Beim stumpfwinkligen Dreieck wird so an die Quadrate jeweils ein Rechteck
„angeklebt“.
Die zentrale Beweisidee ist nun die folgende:
Die beiden in einer Ecke zusammenstoßenden Rechtecke sind flächengleich.
Wenn das so ist, dann folgt daraus unmittelbar der Kosinussatz in seinen
beiden Varianten (wie?).
Dass das so ist, zeigen wir am Beispiel der Ecke C: Die beiden Rechtecke
CGML und CHON sind flächengleich. Die Punkte A, B, L und N liegen
auf einem Kreis (warum?). Die selbe Konstellation, anders gesehen: Die
Geraden AN und BL sind Sekanten dieses Kreises, die sich in C schneiden.
Dann ist die Flächengleichheit der beiden Rechtecke nichts anderes
als die geometrische Einkleidung des Sekantensatzes.
Die "Korrekturflächen" lassen sich mit Hilfe des Kosinus leicht berechnen.
Da cosg > 0 für g < 90° und cos g < 0 für g > 90° ist, kann man beide Aussagen in einer Formel zusammenfassen:
Der Kosinussatz in dieser Form ist ein wichtiges Hilfsmittel, um aus gegebenen Seiten und Winkeln eines Dreiecks die übrigen zu berechnen.