Was gibt es noch im Umfeld des "Pythagoras"?

• Pythagoras meets Diophant (um 250):
  Wie findet man natürliche Zahlen a, b, c, für die c² = a² + b² gilt? Solche Zahlen heißen Pythagoreische Zahlen. Gibt es dafür eine Formel?

• Pythagoras meets Fermat (1601 - 1665):
  Fermat hat bei dem Versuch, Pythagoras zu verallgemeinern, festgestellt: Die Gleichung aⁿ + bⁿ = cⁿ besitzt für n > 2 keine Lösung, die nur aus natürlichen Zahlen a, b, c (>0) besteht. Es hat mehr als 300 Jahre gedauert, bis man ihm endgültig glaubte. "Fermats letzter Satz" - so auch der Titel eines Buchs über die abenteuerliche Geschichte eines mathematischen Rätsels von Simon Singh (1997) - wurde 1993/1995 von dem amerikanischen Mathematiker Andrew Wiles bewiesen.

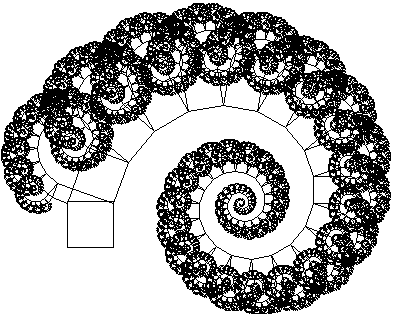
• Pythagoras meets Chaos (2.Hälfte 20. Jhd.):
  Ein Pythagoreisches Fraktal entsteht so: Betrachte jedes Kathetenquadrat als neues Hypotenusenquadrat, wobei das neue rechtwinklige Dreieck zum alten ähnlich ist. Zeichne die neuen Kathetenquadrate. Dann betrachte ... usw.
  Es entstehen faszinierende Bilder.