II.2. Zentrische Streckung

Definition:

Eine geradentreue Abbildung der Ebene auf sich, die einen Fixpunkt S besitzt und jede Gerade g auf eine parallele Gerade g' abbildet, heißt zentrische Streckung.

Einfache Folgerungen aus dieser Definition sind:

Punkt, Bildpunkt und S liegen auf einer Geraden.
Winkel werden in gleich große Winkel abgebildet ("Winkeltreue"). Daraus folgt, dass Dreiecke in ähnliche Dreiecke abgebildet werden.
Sind ein Punkt A (¹ S) und sein Bildpunkt A' bekannt, dann kann man zu jedem anderen Punkt B den Bildpunkt B' wie folgt konstruieren:
- Verbinde A und B, zeichne dazu die Parallele durch A'.
- Zeichne die Gerade durch S und B: Der Schnittpunkt mit der Parallelen ist B'.
Es gibt eine Konstante k (¹ 0), so dass alle Bild-Strecken k-mal so lang sind wie die Original-Strecken. Dabei ist k negativ, wenn S zwischen Punkt und Bildpunkt liegt. Es gibt folgende Fälle:
|k| > 1: Figuren werden vergrößert;
|k| < 1: Figuren werden verkleinert;
k = -1: Punktspiegelung;
k = 1: identische Abbildung.

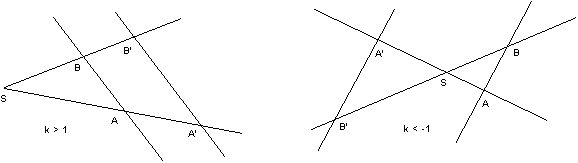
Den Zusammenhang zwischen der Ähnlichkeitslehre und der zentrischen Streckung stiftet der

ś Satz von den zentrisch ähnlichen Dreiecken:

Zwei Dreiecke, deren entsprechende Seiten parallel aber nicht gleich lang sind, lassen sich durch eine zentrische Streckung aufeinander abbilden.

Bitte schalten Sie Java ein, um eine Cinderella-Konstruktion zu sehen.

<< >>