Satz von den drei Spiegelungen

Definition:

Einfache Folgerungen aus der Definition der Bewegung zusammen mit unserem Wissen über Spiegelungen sind:

1. Eine Bewegung bildet geraden-, parallelen-, längen- und winkeltreu ab.
2. Das Bild eines Dreiecks ist ein dazu kongruentes Dreieck. Bei HAF einer geraden Anzahl von Spiegelungen ist der Umlaufsinn von Dreieck und Bild-Dreieck gleich, bei einer ungeraden Anzahl entgegengesetzt.

Satz von den drei Spiegelungen

• Zwei kongruente Dreiecke können durch Hintereinanderausführung von höchstens drei Spiegelungen aufeinander abgebildet werden.
• Sind die Dreiecke gleichsinnig kongruent, reichen zwei Spiegelungen.

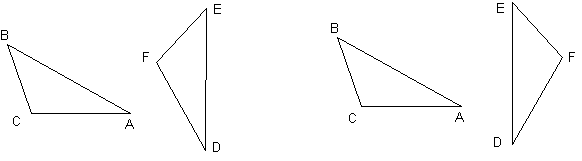
Beweis:

Bitte schalten Sie Java ein, um eine Cinderella-Konstruktion zu sehen.
1. Seien ABC und DEF zwei gleichsinnig kongruente Dreiecke.
    
   1. Spiegelung s₁: Wähle als Spiegelachse die Mittelsenkrechte von AD:
   s₁ bildet A auf D, B auf B' und C auf C' ab; die Dreiecke DB'C' und DEF sind gegensinnig kongruent.
    
   Fallunterscheidung:
   1. B' = E : Dann ist C' ¹ F (wieso?).
      2. Spiegelung s₂ an der Geraden durch DE.
       
   2. B' ¹ E:
      2. Spiegelung s₂ an der Winkelhalbierenden des Winkels B'DE:
      s₂ bildet D auf sich, B' auf E und C' auf C'' ab; die Dreiecke DEC'' und DEF sind gleichsinnig kongruent, also C'' = F.
       
       

 
Bitte schalten Sie Java ein, um eine Cinderella-Konstruktion zu sehen.
2. Seien ABC und DEF zwei gegensinnig kongruente Dreiecke.
    
   1. Spiegelung wie oben
    
   Fallunterscheidung:
    
   1. B' = E : Dann ist C' = F.
      D.h. eine Spiegelung reicht.
       
   2. B' ¹ E:
      2. Spiegelung s₂ an der Winkelhalbierenden des Winkels B'DE:
      s₂ bildet D auf sich, B' auf E und C' auf C'' ab; die Dreiecke DEC'' und DEF sind gegensinnig kongruent, also C'' ¹ F.
       
      3. Spiegelung s₃ an der Geraden durch DE.

<<   >>