Archimedische Körper

Durch passendes "Abschleifen" der Ecken bzw. durch passende Schnitte entstehen aus den Platonischen Körpern neue Körper, deren Flächen zwar auch lauter regelmäßige Vielecke, aber unter Umständen mit verschiedenen Eckenzahlen sind.
Wir wollen sie etwas näher untersuchen, obwohl wir nach dem Klassifikationssatz keine neuen Symmetrie-Gruppen erwarten dürfen.

Definition:

Satz über die Archimedischen Körper

• Die einzigen Archimedischen Körper sind die fünf Platonischen Körpern, die regelmäßigen n-Eck-Säulen (n-Eck-Prismen) mit quadratischen Seitenflächen die regelmäßigen n-eckigen Antiprismen mit gleichseitigen Dreiecken als Seitenflächen und noch weitere 14 Archimedische Körper.

Zum Beweis benutzen wir wie bei den Platonischen Körpern die Summe S der Innenwinkel der Vielecke, die in einer Ecke zusammenstoßen.
Damit eine Raumecke entstehen kann, muss S < 360° sein. Daraus folgt: Jeder Eckenkranz besteht mindestens aus drei und höchstens aus fünf Vielecken.

Die Tabelle gibt einen Überblick über die Innenwinkel in einem regelmäßigen n-Eck.

1) Fünf Vielecke im Eckenkranz

2) Drei Vielecke im Eckenkranz: Die Charakteristik sei (a,b,c) mit a £ b £ c.

Aus S =	(a - 2) × 180°	+	(b - 2) × 180°	+	(c - 2) × 180°	< 360°
	a		b		c

folgt	1	<	1	+	1	+	1	< 3 ×	1	also a < 6 .
	2		a		b		c		a

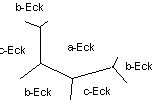Wenn ein Vieleck eine ungerade Ecken- (= Kanten-) Zahl hat, müssen, da alle Eckenkränze kongruent sein sollen, die um dieses Vieleck herum liegenden benachbarten Vielecke alle die gleiche Ecken-Zahl haben;
also wenn a = 3 oder 5 ist, muss b = c sein;
aus a und b ungerade folgt sogar a = b = c.

Für a = 3 ergibt das folgende Möglichkeiten:

Für a = 5 ergibt das folgende Möglichkeiten:

Für a = 4 folgt aus der obigen Ungleichung	1	<	1	+	1	.
	4		b		c

Mit b £ c ergibt das folgende Möglichkeiten:

* Um ein Archimedischer Körper zu sein, muss die n-Eck-Säule quadratische Seitenflächen besitzen.

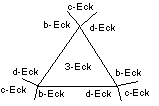3) Vier Vielecke im Eckenkranz: Die Charakteristik sei (a,b,c,d) mit a £ b,c,d.

Aus S < 360° ergibt sich wie im Fall 2)	1 <  4 ×	1	, also a < 4;
		a

d.h. eines der Vielecke muss ein Dreieck sein.

Aus einer ähnliche Überlegung wie oben folgt b = d.

Das ergibt folgende Möglichkeiten:

* Bei diesem Körper stoßen an jeder Ecke ein regelmäßiges n-Eck und drei gleichseitige Dreiecke aneinander. Man kann ihn sich in Analogie zur n-Eck-Säule entstanden denken, nämlich aus einer regelmäßigen n-eckigen Grundfläche und einer dazu kongruenten Deckfläche (E = 2n). Nur liegen die Ecken der Deckfläche nicht senkrecht zur Grundfläche über deren Ecken, sondern die Deckfläche ist soweit um ihren Mittelpunkt gedreht, dass ihre Ecken quasi mittig über den Ecken der Grundfläche liegen und natürlich umgekehrt; so werden jeder Ecke der einen Fläche zwei Ecken der anderen zugeordnet (K = 2n + 2n). Damit entsteht ein Kranz von 2n Dreiecken als Seitenflächen (F = 2 + 2n). Ein solcher Körper heißt Antiprisma. Die dreieckigen Seitenflächen des Antiprismas müssen gleichseitig sein, wenn es sich um einen Archimedischen Körper handeln soll.

Mit den in den Tabellen aufgezeigten Fällen scheinen alle Möglichkeiten erschöpft: Ein 14. neuer Archimedischer Körper scheint unmöglich. Der Denkfehler: Wir haben die Körper durch ihre kongruenten Eckenkränze charakterisiert. Die Eckenkränze bestimmen aber nicht eindeutig den Archimedischen Körper. Erst 1934 entdeckte man, dass es zu der Charakteristik (3,4,4,4) zwei nicht kongruente Archimedische Körper gibt. Das ist allerdings der einzige Fall, wo es zu einer Charakteristik zwei nicht kongruente Körper gibt.

<<   >>